Introductory Biophysics Course · C004229


Contents
- Learning to understand feedback: what is positive and what is negative feedback
- Converting a system into a differential equation: learning to convert words into mathematics
- In this course we will model the following systems: population models, feather and friction systems, prey hunter systems, chemical reactions, epidemiology (such as learning to model the Corona virus), neurons, pest outbreak, respiration, food chains, and many others
- Calculate trajectories of the evolution of the state of a system, via Euler integration
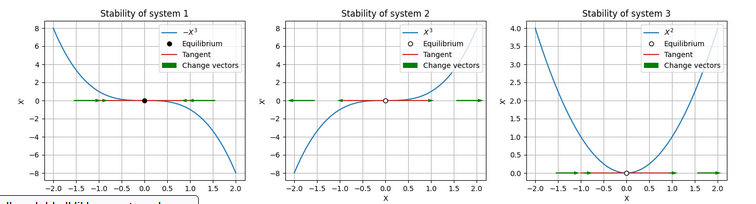
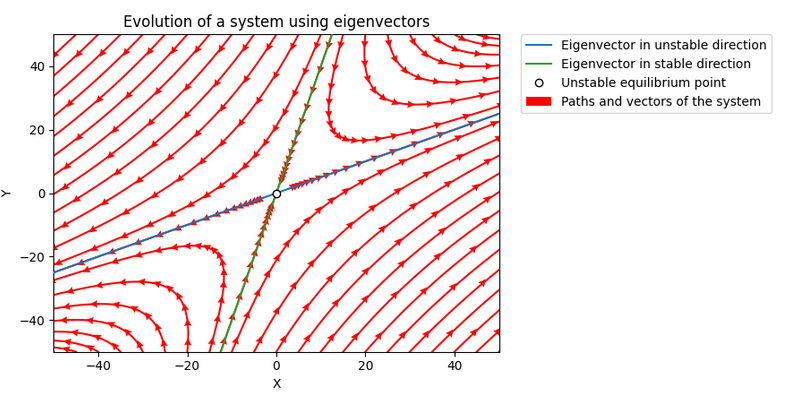
- Recognize types of equilibria: stable knots, unstable knots, saddle points, stable and unstable coils
- Method of the nullclines
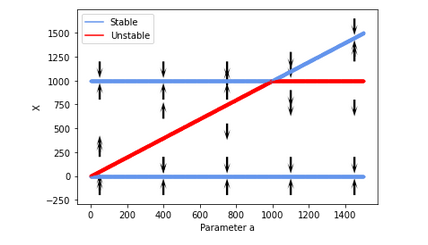
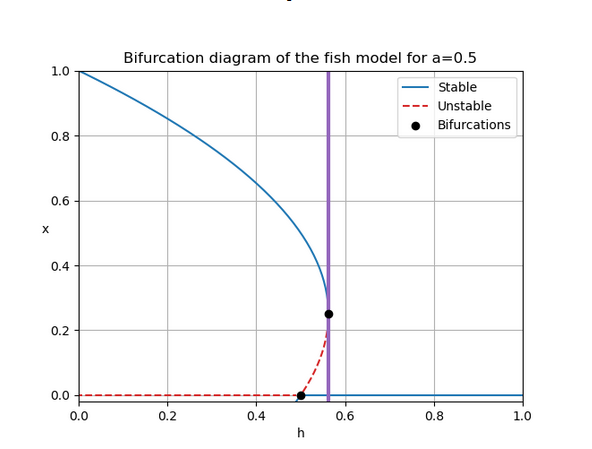
- Recognize bifurcations of equilibria: transcritical bifurcation, saddle-node bifurcation, pitch fork bifurcation
- Recognizing oscillations in systems: in chemistry, biology and physiology
- Hopf bifurcation: the creation of limit cycles
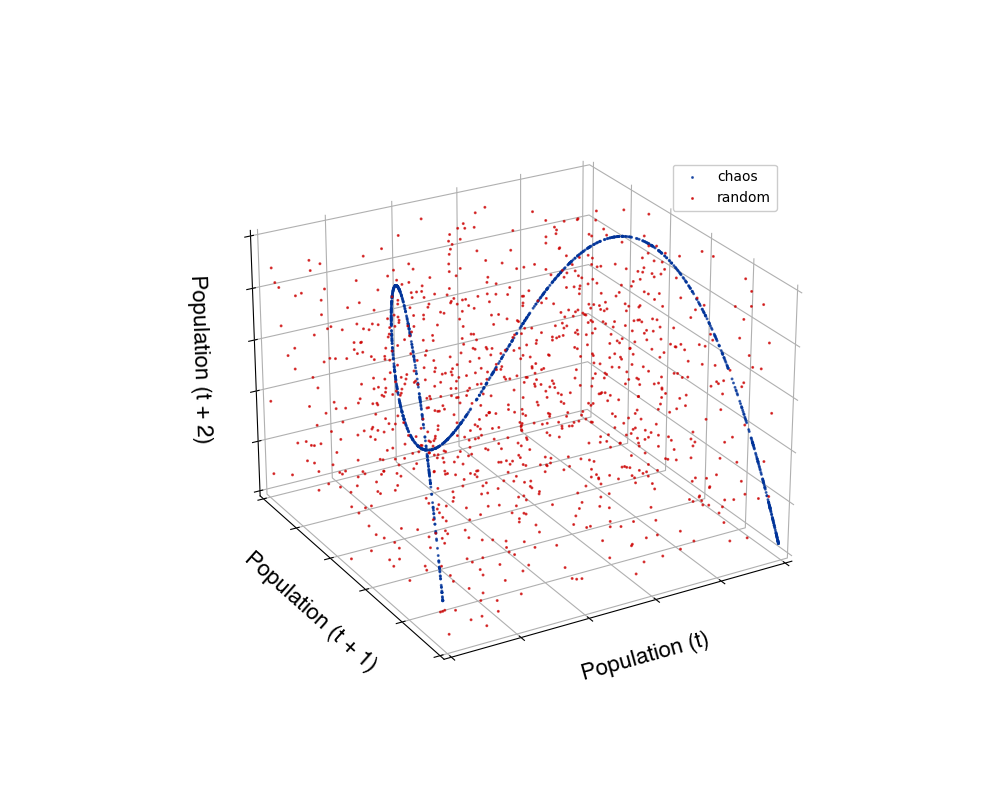
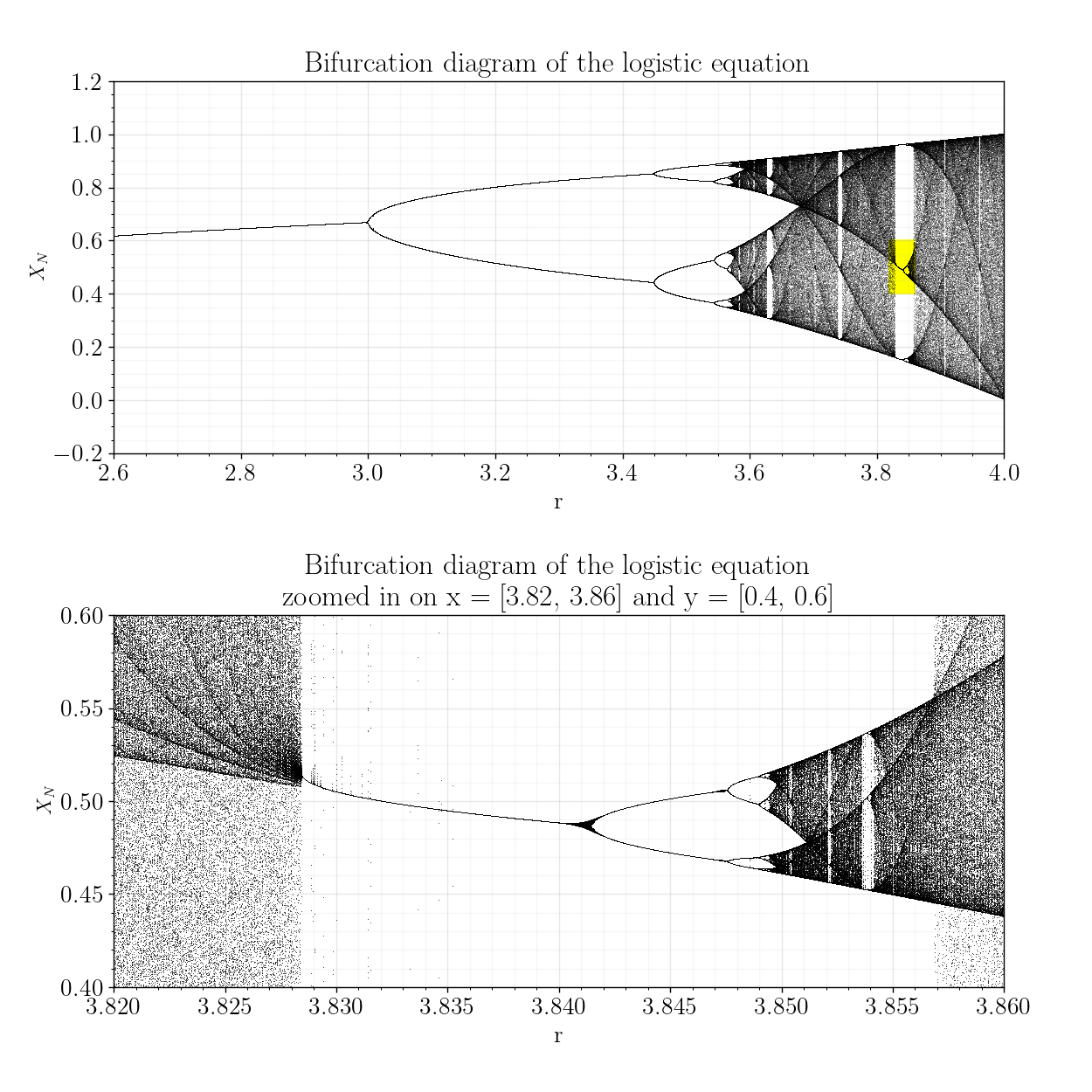
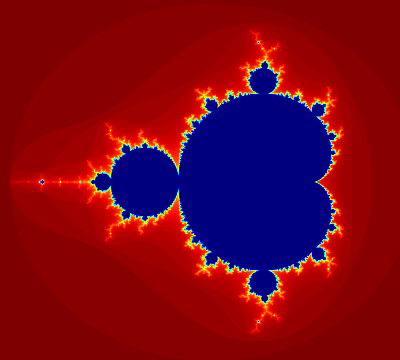
- Chaos: in continuous models and in discrete models. Learning to recognize the properties of choas, understanding the routes to a chaotic system
To accomplish this, we will use Python. Apart from plain Python, we will use the Numpy, Sympy and Scipy packages for calculations and Matplotlib to create professional figures.
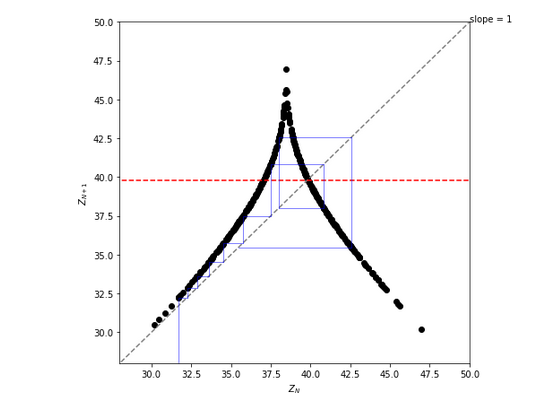
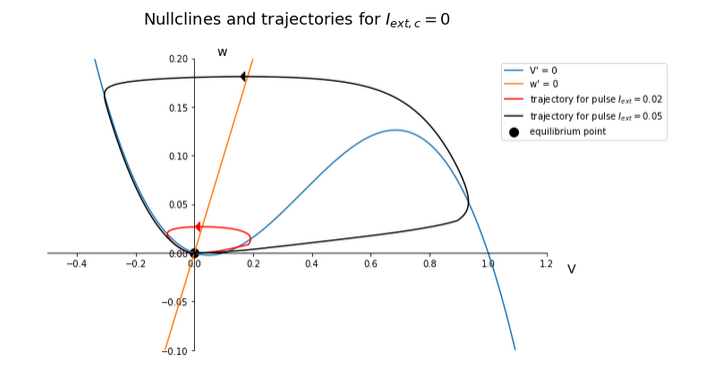
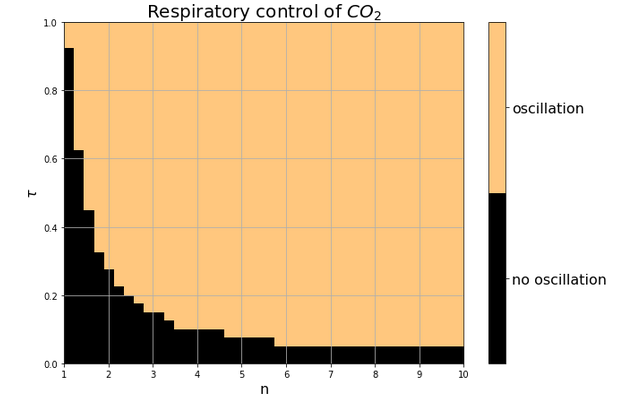
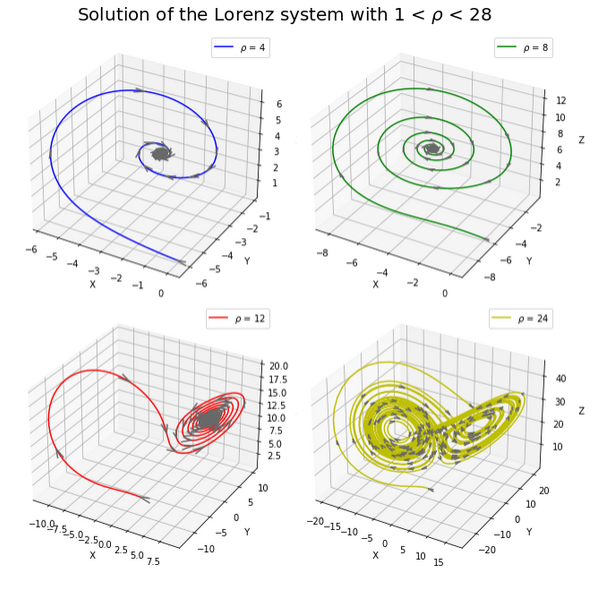
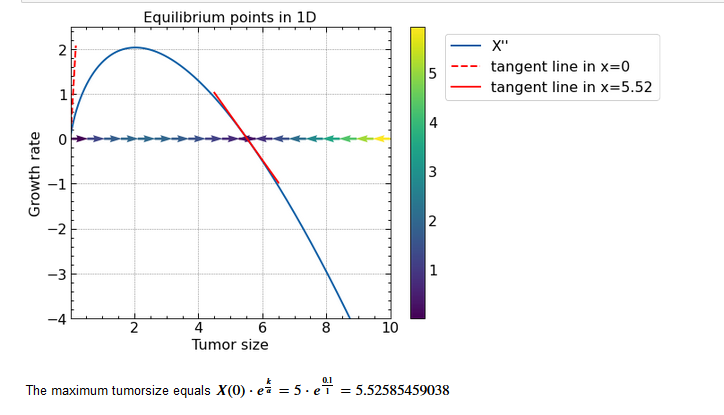
Some images made by our students in previous years: